3.1. The approximate function of optimal intervals
Piotr Wozniak 1990
This text was taken from P.A.Wozniak, Optimization of learning, Master’s Thesis, University of Technology in Poznan, 1990. It was spell-checked, and the terminology was adjusted for publication at supermemo.com. Square brackets include comments added later. Archive figures at the bottom were added in 2004.
| 3. Account of research leading to the SuperMemo method 3.1. The approximate function of optimal intervals |
It was 1982 when I made my first observations concerning the mechanism of memory that were later used in the formulation of the SuperMemo method. As a then student of molecular biology I was overwhelmed by the amount of knowledge that was required to pass exams in mathematics, physics, chemistry, biology, etc. The problem was not in being unable to master the knowledge. Usually 2-3 days of intensive studying were enough to pack the head with data necessary to pass an exam. The frustrating point was that only an infinitesimal fraction of newly acquired wisdom could remain in memory after few months following the exam.
My first observation, obvious for every attentive student, was that one of the key elements of learning was active recall. This observation implies that passive reading of books is not sufficient if it is not followed by an attempt to recall learned facts from memory. The principle of basing the process of learning on recall will be later referred to as the active recall principle. The process of recalling is much faster and not less effective if the questions asked by the student are specific rather than general. It is because answers to general questions contain redundant information necessary to describe relations between answer subcomponents.
To illustrate the problem let us imagine an extreme situation in which a student wants to master knowledge contained in a certain textbook, and who uses only one question in the process of recall: What did you learn from the textbook? Obviously, information describing the sequence of chapters of the book would be helpful in answering the question, but it is certainly redundant for what the student really wants to know. The principle of basing the process of recall on specific questions will be later referred to as the minimum information principle. This principle appears to be justified not only because of the elimination of redundancy.
Having the principles of active recall and minimum information in mind, I created my first databases (i.e. collections of questions and answer) used in an attempt to retain the acquired knowledge in memory. At that time the databases were stored in a written form on paper. My first database was started on June 6, 1982, and was composed of pages that contained about 40 pairs of words each. The first word in a pair (interpreted as a question) was an English term, the second (interpreted as an answer) was its Polish equivalent. I will refer to these pairs as items.
I repeated particular pages in the database in irregular intervals (dependent mostly on the availability of time) always recording the date of the repetition, items that were not remembered and their number. This way of keeping the acquired knowledge in memory proved sufficient for a moderate-size database on condition that the repetitions were performed frequently enough.
In November 1983, my first English database reached 1000 items and the irregular repetitions became annoyingly inefficient. At this time, I started creating a database dealing with human biology (Nov 23, 1983). It later appeared that items in the human biology database were much more difficult to remember than those in the English database, and the process of increasing the size of my databases gradually progressed at the cost of knowledge retention, i.e. a decreasing fraction of knowledge was kept in memory. By the end of 1984, having a constant opportunity to observe the impact of repetition spacing on the effectiveness of learning, I had a new idea ready about how to improve the learning process. It is worth noting that at this time, I had about 3000 items in the English and 1400 items in the biology database. I then estimated my knowledge retention to be 60 and 40 percent respectively, while the time spent on repetitions amounted to about 10 and 4 minutes per day. This meant that I worked at a rate of 120 items/year/minute (i.e. every minute of work per day provided 120 items memorized each year). The retention figures were low enough to disqualify such a learning method!
A great deal of experimental data obtained during my initial work with knowledge retention databases make a valuable study material which until now has not yet been fully interpreted (see Chapter 11). Irregular length of intervals provides an interesting insight into the process of memory retention and forgetting. [a model of intermittent learning has finally been proposed in 2005 and is described in Building memory stability through rehearsal]
At the beginning of 1985 I designed two experiments which consequently revolutionized my learning methodology and lead to the formulation of the SuperMemo method.
The first experiment can be a good illustration of how a misconceived idea can yield valuable conclusions. It is a common intuition, that with successive repetitions, knowledge should gradually become more durable and require less frequent review. Thus repetitions separated by increasing intervals should be more effective than those whose intervals are always the same. This belief proved to be false. Let us see an experiment which demonstrates the fact:
Experiment on the influence of various repetition spacing patterns on the effect of repetitions on knowledge retention (Jan 31, 1985 – Aug 2, 1986)
- The memorized knowledge consisted of 195 items divided into three equal groups: A, B and C.
- Each of the items had the following form:
Question: English irregular verb
Answer: simple present, simple past and past participle forms of the verb in question - All items of a particular group were memorized at one session by repeating them until all were known (group A – Jan 31, B – Feb 2, C – Feb 3).
- Two final control dates were established: Dec 6-7, 1985 and Aug 1-2, 1986 on which the level of retention in all groups was measured at the same time (for each item the accuracy of recall was measured in a four grade scale).
- Before the control dates, all of the groups A, B and C underwent 6 independent repetitions in the following intervals:
| Repetition number | Group A(equal spacing over longer time: 108 days) | Group B(spacing based on increasing intervals) | Group C(equal spacing in 30 days) |
| 1 | 18 days | 1 day | 5 days |
| 2 | 18 days | 5 days | 5 days |
| 3 | 18 days | 9 days | 5 days |
| 4 | 18 days | 24 days | 5 days |
| 5 | 18 days | 44 days | 5 days |
| 6 | 18 days | 70 days | 5 days |
The intention of the experiment was to prove that increasing intervals are the best for memory consolidation (group B) as opposed to intervals that are evenly distributed (group A) or concentrated in time (group C). The results of the experiment are shown in Fig.3.1:
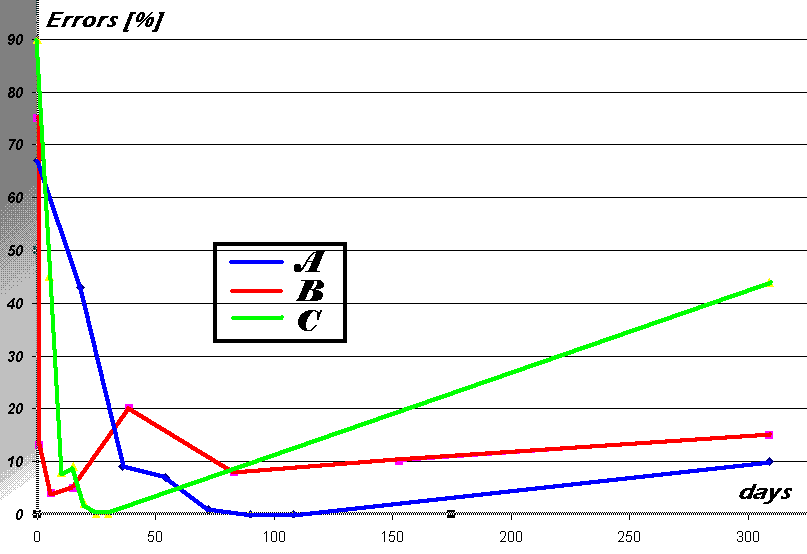
(The results of the second control are not present on the graph because of the prosaic fact that studying at the University of Technology [started in October 1985] required perfect knowledge of irregular verbs, therefore another measurement was pointless)
As it can be seen in Fig.3.1., the experiment yielded unexpected results proving that increasing inter-repetition intervals need not be better than constant-length intervals. Fortunately, long before the results of the experiment were known, I suspected that there must exist optimum inter-repetition intervals. The principle of using such intervals in the process of learning will be later be referred to as the optimum repetition spacing principle.
The following experiment was to confirm the existence of optimum inter-repetition intervals and to estimate their length.
Experiment intended to approximate the length of optimum inter-repetition intervals (Feb 25, 1985 – Aug 24, 1985):
- The experiment consisted of stages A, B, C, … etc. Each of these stages was intended to calculate the second, third, fourth and further quasi-optimal inter-repetition intervals (the first interval was set to one day as it seemed the most suitable judging from the data collected earlier). The criterion for establishing quasi-optimal intervals was that they should be as long as possible and allow for not more than 5% loss of remembered knowledge.
- The memorized knowledge in each of the stages A, B, C, consisted of 5 pages containing about 40 items in the following form:
Question: English word,
Answer: its Polish equivalent. - Each of the pages used in a given stage was memorized in a single session and repeated next day. To avoid confusion note, that in order to simplify further considerations I use the term first repetition to refer to memorization of an item or a group of items. After all, both processes, memorization and relearning, have the same form – answering questions as long as it takes for the number of errors to reach zero.
- In the stage A (Feb 25 – Mar 16), the third repetition was made in intervals 2, 4, 6, 8 and 10 days for each of the five pages respectively. The observed loss of knowledge after these repetitions was 0, 0, 0, 1, 17 percent respectively. The seven-day interval was chosen to approximate the second quasi-optimal inter-repetition interval separating the second and third repetitions.
- In the stage B (Mar 20 – Apr 13), the third repetition was made after seven-day intervals whereas the fourth repetitions followed in 6, 8, 11, 13, 16 days for each of the five pages respectively. The observed loss of knowledge amounted to 3, 0, 0, 0, 1 percent. The 16-day interval was chosen to approximate the third quasi-optimal interval. NB: it would be scientifically more valid to repeat the stage B with longer variants of the third interval because the loss of knowledge was little even after the longest of the intervals chosen; however, I was then too eager to see the results of further steps to spend time on repeating the stage B that appeared sufficiently successful (i.e. resulted in good retention)
- In the stage C (Apr 20 – Jun 21), the third repetitions were done after seven-day intervals, the fourth repetitions after 16-day intervals and the fifth repetitions after intervals of 20, 24, 28, 33 and 38 days. The observed loss of knowledge was 0, 3, 5, 3, 0 percent. The stage C was repeated for longer intervals preceding the fifth repetition (May 31 – Aug 24). The intervals and memory losses were as follows: 32-8%, 35-8%, 39-17%, 44-20%, 51-5% and 60-20%. The 35-day interval was chosen to approximate the fourth quasi-optimal interval.
It is not difficult to notice, that each of the stages of the described experiment took about twice as much time as the previous one. It could take several years to establish first ten quasi-optimal inter-repetition intervals. Indeed, I continued experiments of this sort in following years in order to gain deeper understanding of the process of optimally spaced repetitions of memorized knowledge. However, at that time (Aug 24, 1985), I decided to employ the findings in my day-to-day process of routine learning.
Algorithm SM-0 used in spaced repetition without a computer (Aug 25, 1985)
- Split the knowledge into smallest possible items
- Associate items into groups containing 20-40 elements. These groups are later called pages
- Repeat whole pages using the following intervals (in days):
- I(1)=1
- I(2)=7
- I(3)=16
- I(4)=35
- for i>4: I(i):=I(i-1)*2
where I(i) is the interval used after the i-th repetition.
- Copy all items forgotten after the 35 day interval into newly created pages (without removing them from previously used pages). Those new pages will be repeated in the same way as pages with items learned for the first time
Note, that inter-repetition intervals after the fifth repetition were assumed to increase twice in subsequent repetitions. This fact was based on intuition rather than on experiment. In two years of using the Algorithm SM-0 sufficient data were collected to confirm a reasonable accuracy of this assumption [see also: Building memory stability through rehearsal section 4: ” Memory is optimized to meet probabilistic properties of the environment”]. For the detailed description of the paper-based variant of the SuperMemo method (derived from the Algorithm SM-0) see Chapter 7 [click here for a newer version of the same text].
Upon formulating it, I started using the Algorithm SM-0 to learn English on Aug 25, 1985. I also employed it in learning biology as of Oct 1, 1985. In the latter case with slightly shorter intervals as the biological knowledge appeared to be slightly more difficult to remember. For the first time, I was able to reconcile high knowledge retention with infrequent repetitions that in consequence lead to steadily increasing volume of knowledge remembered without the necessity to increase the timeload!
Retention of 80% was easily achieved, and could even be increased by shortening the inter-repetition intervals. This, however, would involve more frequent repetitions and, consequently, increase the timeload. The assumed repetition spacing provided a satisfactory compromise between retention and workload. The next significant improvement of the Algorithm SM-0 was to come only in 1987 after the application of a computer to supervise the learning process. In the meantime, I accumulated about 7190 and 2817 items in my new English and biological databases respectively. With the estimated working time of 12 minutes a day for each database, the average knowledge acquisition rate amounted to 260 and 110 items/year/minute respectively, while knowledge retention amounted to 80% at worst.
Although the acquisition rate may not have seemed staggering, the Algorithm SM-0 was revolutionary in comparison to my previous methods because of two reasons:
- with the lapse of time, knowledge retention increased instead of decreasing (as it was the case with intermittent learning)
- in a long perspective, the acquisition rate remained almost unchanged (with intermittent learning, the acquisition rate would decline substantially over time)
[to see a detailed description of the first SuperMemo algorithm see: Using SuperMemo without a computer (1992)]
[this archive section was added in 2004]
20 years later …
This scan of my 1982 notes shows the first attempts to record recall data following repetitions at varying intervals:
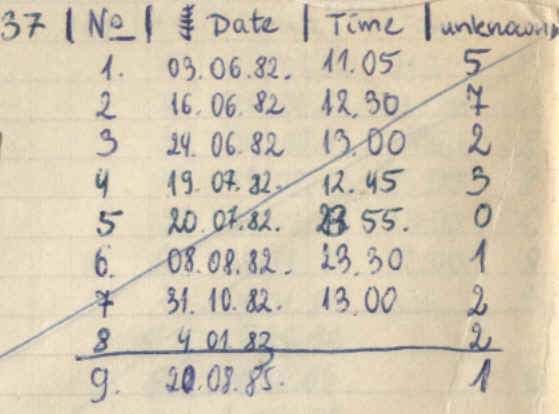
My first experiments were run in parallel with learning human biology and English vocabulary (here English-Polish word pairs on a starting page from June 3, 1982):




